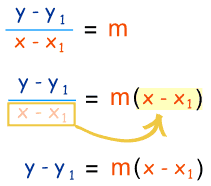Let’s be honest , math formulas can feel intimidating, especially when you first meet something like the point slope form. It sounds complicated, but once you break it down, it’s surprisingly logical and even kind of fun. Whether you’re a student trying to pass algebra, a parent helping with homework, or someone brushing up on math skills, understanding this concept will make a big difference.
In simple terms, the point slope form helps you write the equation of a straight line when you know one point on the line and its slope. That’s it! It’s one of the most practical tools in algebra because it connects the geometric idea of a line to its algebraic formula.
In this guide, we’ll walk through what the point slope form is, how to use it, convert it to other forms, and even solve real-world problems. By the end, you’ll not only “get it” , you’ll be able to explain it to others.
What Is the Point Slope Form?
At its core, the point slope form is a way to represent the equation of a line. It tells you how to find all the points on a line if you know just one point and the line’s slope.
The formula looks like this:
y – y₁ = m(x – x₁)
Where:
- (x₁, y₁) = a specific point on the line
- m = the slope (rate of change)
- (x, y) = any point on the line
That’s it. You plug in the slope and a point, and you have your equation. It’s like a map telling you how to find every other point on that line.
Breaking Down the Formula
Let’s slow down and understand each piece.
1. The Slope (m)
The slope tells you how steep a line is. It’s the ratio of the vertical change (rise) to the horizontal change (run).
Formula:
m = (y₂ – y₁) / (x₂ – x₁)
If the slope is:
- Positive, the line goes upward (left to right)
- Negative, the line goes downward
- Zero, it’s flat (horizontal line)
- Undefined, it’s vertical (no run)
2. The Point (x₁, y₁)
This is a specific point on the line. Think of it as your anchor ,once you know one point and the slope, you can predict the entire line.
3. The Variables (x, y)
These represent any other point on the same line. They’re the unknowns you solve for when you graph or calculate coordinates.
Why Use Point Slope Form?
You might wonder,why not just use the regular y = mx + b form everyone talks about? Good question.
Here’s why point slope form is special:
- It’s faster when you already know one point and the slope.
- It’s flexible ,perfect for writing equations before you find the y-intercept.
- It’s a stepping stone , you can easily convert it to slope-intercept or standard form later.
In short, it’s like the “in-progress” version of a line equation that still works beautifully.
How to Use Point Slope Form (Step-by-Step)
Let’s walk through it step by step. You’ll see how easy it can be once you get the hang of it.
Step 1: Identify the Point and the Slope
Say you know:
- A point (x₁, y₁) = (2, 3)
- A slope m = 4
Step 2: Plug Values into the Formula
Use the formula y – y₁ = m(x – x₁).
Substitute:
y – 3 = 4(x – 2)
That’s it! You now have the point slope form equation.
Step 3: Simplify (Optional)
If you prefer slope-intercept form (y = mx + b), expand and simplify:
y – 3 = 4x – 8
y = 4x – 5
And there you go — the same line, just in a different format.
Real-Life Example of Point Slope Form
Imagine you’re designing a ramp. You want the ramp to rise 2 feet for every 6 feet it runs horizontally. That’s a slope of 2/6, or 1/3.
If the ramp starts at the point (0, 0), your equation becomes:
y – 0 = (1/3)(x – 0)
Simplified:
y = (1/3)x
Now you can calculate how high the ramp will be at any distance.
For example, if the ramp runs 12 feet, plug in x = 12:
y = (1/3)(12) = 4
So the ramp will rise 4 feet after 12 feet of horizontal run.
That’s point slope form in action — simple and practical.
How to Graph Using Point Slope Form
Graphing using point slope form is super simple.
- Plot the given point (x₁, y₁).
- Use the slope (m) to find another point. Remember: slope = rise/run.
- Draw a straight line through both points.
Example:
Equation: y – 2 = (3/2)(x – 4)
- Start at (4, 2).
- Rise = 3, Run = 2 → go up 3 units, right 2 units.
- Plot the new point (6, 5).
- Connect them — that’s your line!
Converting Between Forms
One reason the point slope form is so useful is that it’s easy to switch between formats.
1. To Slope-Intercept Form (y = mx + b)
Example:
y – 5 = 2(x – 3)
Simplify:
y – 5 = 2x – 6
y = 2x – 1
2. To Standard Form (Ax + By = C)
Take the same equation:
y – 5 = 2x – 6
Rearrange:
2x – y = 1
That’s the standard form.
Common Mistakes to Avoid
Even though point slope form is straightforward, students often make small errors. Let’s fix those before they happen.
- Forgetting parentheses around (x – x₁).
- Wrong: y – 2 = 3x – 4
- Correct: y – 2 = 3(x – 4)
- Using the wrong signs.
If the point is (–3, 4):- Formula → y – 4 = m(x + 3)
- Mixing up slope direction.
Always remember: slope = rise/run → (vertical over horizontal). - Not simplifying properly when converting to other forms.
- Forgetting units in real-world problems (e.g., feet, seconds, miles).
Understanding Slope Conceptually
To really “get” point slope form, you need to understand slope itself.
What Slope Tells You
Slope shows how one variable changes compared to another. For instance:
- In physics, it can represent speed (distance over time).
- In business, it can show cost increases (price over quantity).
- In daily life, it can represent a hill’s steepness.
So when you use slope in an equation, you’re describing a consistent rate of change, the foundation of linear relationships.
When to Use Point Slope Form vs. Other Forms
You’ve got three main line forms:
- Point Slope Form: y – y₁ = m(x – x₁)
- Slope Intercept Form: y = mx + b
- Standard Form: Ax + By = C
Here’s when to use each:
| Situation | Best Form |
|---|---|
| You know one point and slope | Point Slope |
| You know slope and y-intercept | Slope Intercept |
| You want to eliminate fractions | Standard |
If you start with a point and slope, go for point slope form. Later, you can simplify into other forms if needed.
Using Point Slope Form in Real Life
Let’s make this relatable with a few scenarios:
- Predicting costs – Suppose a taxi charges a $3 base fare and $2 per mile.
If at 2 miles, cost = $7 → slope = 2, point = (2, 7): y – 7 = 2(x – 2) - Tracking fitness progress – You run 1 mile in 10 minutes, and after training, 3 miles in 24 minutes.
Slope = (24 – 10) / (3 – 1) = 14/2 = 7
That’s your rate: 7 minutes per mile. - Planning budgets – You spend $200 in 4 weeks and $300 in 6 weeks.
Slope = (300 – 200) / (6 – 4) = 50
That’s $50 per week.
All of these situations describe a linear relationship, which the point slope form helps represent clearly.
How Point Slope Form Helps in Problem Solving
Understanding this formula gives you confidence in algebra and data interpretation. You can:
- Create equations from real data points
- Compare rates of change
- Transition easily into calculus and advanced math
Once you grasp the logic behind it, the math becomes intuitive — it’s about describing change in a clear, consistent way.
Tips to Master Point Slope Form
Here are some quick tips to keep in mind:
- Always start with what you know.
Identify your slope and one point. - Write the formula before substituting.
That way, you won’t misplace numbers. - Use parentheses.
They’re essential for keeping signs correct. - Check your slope.
Make sure it’s accurate before plugging it in. - Double-check conversions.
Going from one form to another? Simplify step by step.
Conclusion: Why Point Slope Form Just Works
The point slope form isn’t just another formula, it’s a way to make sense of how things change. Whether you’re studying algebra or applying math to real-world problems, this method helps you describe a line using simple, logical parts: one point and a slope.
Remember, math doesn’t have to be scary or complicated. Once you understand what each part means, the equation becomes a story, about direction, movement, and relationships between quantities. So next time you face a line equation, you’ll know exactly where to start.
Question for you:
What’s one real-life situation where you could use point slope form to predict or describe something?
FAQs About Point Slope Form
1. What is the point slope form used for?
It’s used to write the equation of a line when you know one point on the line and its slope.
2. How do I find the slope from two points?
Use m = (y₂ – y₁) / (x₂ – x₁) to calculate the slope between any two points.
3. Can I convert point slope form to y = mx + b?
Yes! Just distribute the slope and simplify.
4. What if the line is vertical?
A vertical line has an undefined slope, so you write it as x = a constant instead.
5. What if the slope is zero?
That means it’s a horizontal line, and the equation is simply y = constant.
6. Why is point slope form better for some problems?
Because it’s quick and direct when you already know a point and slope.
7. Can I graph directly from point slope form?
Absolutely! Start at your given point, then use the slope to find other points.
8. What’s the difference between slope and y-intercept?
Slope measures change; the y-intercept shows where the line crosses the y-axis.
9. Can I use fractions for slope?
Yes . and in fact, fractions help visualize “rise over run” clearly.
10. Do I need to simplify the equation?
Not always. Point slope form is already complete, but simplifying can make it easier to read or graph.